All leaked interview problems are collected from Internet.
142. Linked List Cycle II
Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
Note: Do not modify the linked list.
Follow up:
Can you solve it without using extra space?
Approach #1 Hash Table [Accepted]
Intuition
If we keep track of the nodes that we've seen already in a Set, we can
traverse the list and return the first duplicate node.
Algorithm
First, we allocate a Set to store ListNode references. Then, we traverse
the list, checking visited for containment of the current node. If the node
has already been seen, then it is necessarily the entrance to the cycle. If
any other node were the entrance to the cycle, then we would have already
returned that node instead. Otherwise, the if condition will never be
satisfied, and our function will return null.
The algorithm necessarily terminates for any list with a finite number of
nodes, as the domain of input lists can be divided into two categories:
cyclic and acyclic lists. An acyclic list resembles a null-terminated chain
of nodes, while a cyclic list can be thought of as an acyclic list with the
final null replaced by a reference to some previous node. If the while
loop terminates, we return null, as we have traversed the entire list
without encountering a duplicate reference. In this case, the list is
acyclic. For a cyclic list, the while loop will never terminate, but at
some point the if condition will be satisfied and cause the function to
return.
Complexity Analysis
- Time complexity :
For both cyclic and acyclic inputs, the algorithm must visit each node
exactly once. This is transparently obvious for acyclic lists because the
th node points to null, causing the loop to terminate. For cyclic
lists, the if condition will cause the function to return after
visiting the th node, as it points to some node that is already in
visited. In both cases, the number of nodes visited is exactly ,
so the runtime is linear in the number of nodes.
- Space complexity :
For both cyclic and acyclic inputs, we will need to insert each node into
the Set once. The only difference between the two cases is whether we
discover that the "last" node points to null or a previously-visited
node. Therefore, because the Set will contain distinct nodes, the
memory footprint is linear in the number of nodes.
Approach #2 Floyd's Tortoise and Hare [Accepted]
Intuition
What happens when a fast runner (a hare) races a slow runner (a tortoise) on a circular track? At some point, the fast runner will catch up to the slow runner from behind.
Algorithm
Floyd's algorithm is separated into two distinct phases. In the first
phase, it determines whether a cycle is present in the list. If no cycle is
present, it returns null immediately, as it is impossible to find the
entrance to a nonexistant cycle. Otherwise, it uses the located "intersection
node" to find the entrance to the cycle.
Phase 1
Here, we initialize two pointers - the fast hare and the slow tortoise.
Then, until hare can no longer advance, we increment tortoise once and
hare twice.1 If, after advancing them, hare and tortoise point to
the same node, we return it. Otherwise, we continue. If the while loop
terminates without returning a node, then the list is acyclic, and we return
null to indicate as much.
To see why this works, consider the image below:
Here, the nodes in the cycle have been labelled from 0 to , where
is the length of the cycle. The noncyclic nodes have been labelled from
to -1, where is the number of nodes outside of the cycle. After
iterations, tortoise points to node 0 and hare points to some node
, where . This is because hare traverses
nodes over the course of iterations, exactly of which are in the
cycle. After more iterations, tortoise obviously points to node
, but (less obviously) hare also points to the same node. To see why,
remember that hare traverses from its starting position of :
Therefore, given that the list is cyclic, hare and tortoise will
eventually both point to the same node, known henceforce as the
intersection.
Phase 2
Given that phase 1 finds an intersection, phase 2 proceeds to find the node
that is the entrance to the cycle. To do so, we initialize two more pointers:
ptr1, which points to the head of the list, and ptr2, which points to
the intersection. Then, we advance each of them by 1 until they meet; the
node where they meet is the entrance to the cycle, so we return it.
Use the diagram below to help understand the proof of this approach's correctness.
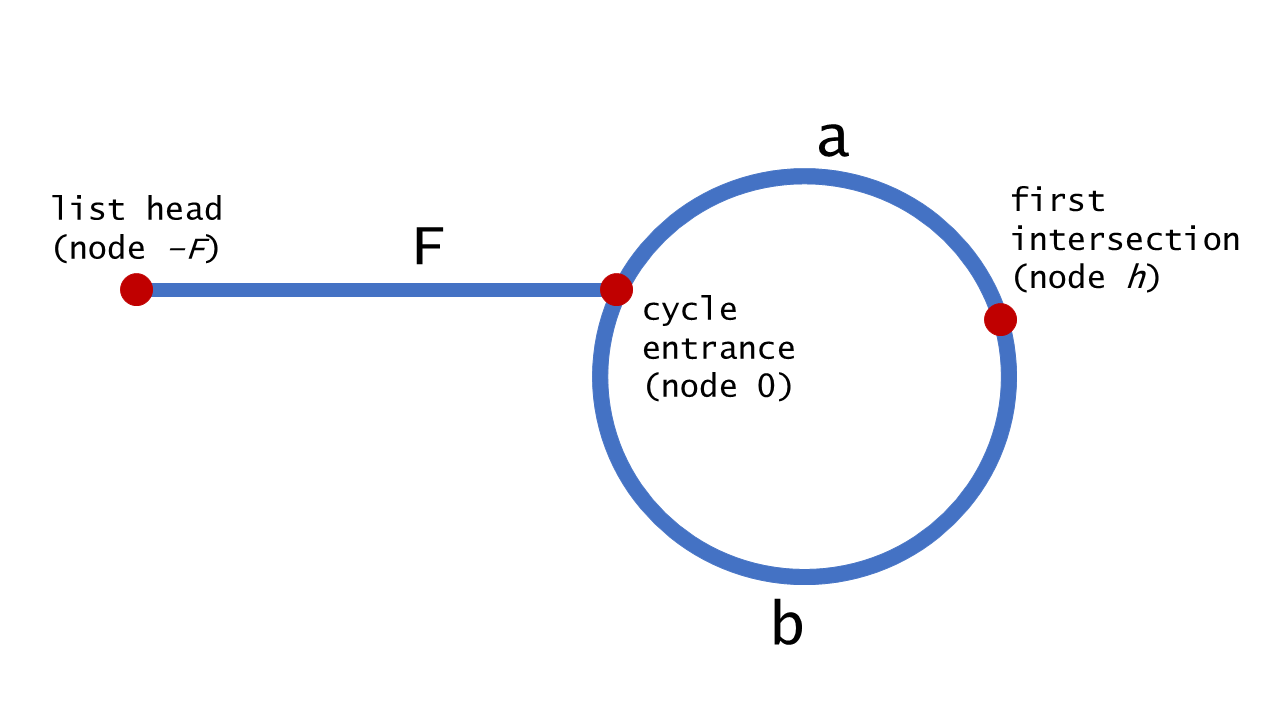
We can harness the fact that hare moves twice as quickly as tortoise to
assert that when hare and tortoise meet at node , hare has
traversed twice as many nodes. Using this fact, we deduce the following:
Because , pointers starting at nodes and will traverse the same number of nodes before meeting.
To see the entire algorithm in action, check out the animation below:
!?!../Documents/142_Linked_List_Cycle_II.json:1280,720!?!
Complexity Analysis
-
Time complexity :
For cyclic lists,
hareandtortoisewill point to the same node after iterations, as demonstrated in the proof of correctness. , so phase 1 runs in time. Phase 2 runs for iterations, so it also runs in time.For acyclic lists,
harewill reach the end of the list in roughly iterations, causing the function to return before phase 2. Therefore, regardless of which category of list the algorithm receives, it runs in time linearly proportional to the number of nodes. -
Space complexity :
Floyd's Tortoise and Hare algorithm allocates only pointers, so it runs with constant overall memory usage.
Footnotes
Analysis and solutions written by: @emptyset
Proof of phase 1 inspired by paw88789's answer here.
Proof of phase 2 inspired by Old Monk's answer here.
-
It is sufficient to check only
harebecause it will always be ahead oftortoisein an acyclic list. ↩